Chapitre 2: Les intégrales curvilinges §

Définition 2.1: Courbes régulières, courbes simples régulières, paramétrisation §

$\Gamma \subseteq {\mathbb{R}}^n$ est une courbe régulière si il existe $[a,b]\subseteq \mathbb{R}$ et une fonction $\gamma [a,b]\to {\mathbb{R}}^n:t\to \gamma (t)={\gamma }_1(t),...{\gamma }_n(t)$ telle que

1. $\gamma ([a,b])=\{x\in {\mathbb{R}}^n:\exists t\in [a,b]\mathrm{avec}\gamma (t)=x\}=\Gamma$
2. $\gamma \in C^1([a,b];{\mathbb{R}}^n)$
3. $\Vert {\gamma }^{\prime }\left(t\right)\Vert =\sqrt{{\sum }_{j=1}^n{\left({\gamma }_j^{\prime }\left(t\right)\right)}^2}\ne 0$ $\gamma$ est alors une paramétrisation de $\Gamma$ De plus $\Gamma$ est une courbe simple s’il existe une paramétrisation de $\Gamma$ telle que $\gamma$ est injective sur $[a,b[$ De plus $\Gamma$ est une courbe fermée si toutes les paramétrisations régulières de $\Gamma$ vérifient que $\gamma (a)=\gamma (b)$ On dit que $\Gamma$ est une courbe régulière par morceaux si $\Gamma ={\Gamma }_1\cup \dots \cup {\Gamma }_k$ où les ${\Gamma }_i$ sont des courbes régulières

Définition 2.4 : Intégrale curviligne §

Soient $\Omega \subset {\mathbb{R}}^n$ un ensemble ouvert $\Gamma \subset \Omega$ une courbe régulière, et $\gamma :[a,b]\to \Gamma$ une paramétrisation de cette courbe. Pour $f\in C^0(\Omega )$ , nous définissons l’intégrale curviligne de $f$ le long de $\Gamma$:

$${\int }_{\Gamma }fd\ell ={\int }_a^{b}f(\gamma (t))\Vert {\gamma }^{\prime }(t)\Vert dt$$

Pour un champ vectoriel $F\in C^0(\Omega ,{\mathbb{R}}^n)$ nous définissons :

$${\int }_{\Gamma }Fd\ell ={\int }_{\Gamma }F\bullet d\ell ={\int }_a^{b}F(\gamma (t))\bullet {\gamma }^{\prime }(t)dt$$

Si $\Gamma ={\bigcup }_{i=1}^k{\Gamma }_k$

$${\int }_{\Gamma }fd\ell =\sum _{i=1}^k{\int }_{{\Gamma }_i}fd\ell \text{et}{\int }_{\Gamma }F\bullet d\ell =\sum _{i=1}^k{\int }_{{\Gamma }_i}F\bullet d\ell$$

Remarque 2.5: Sens et longueur §

1. Pour une courbe régulière $\Gamma$, on définit sa longueur par

$$\text{long }\Gamma ={\int }_{\Gamma }1d\ell$$

2. La notion d’intégrale curviligne d’un champs scalaire est indépendante du choix de paramétrisation. Par contre la notion d’intégrale curviligne d’un champs non scalaire est indépendante du choix de paramétrisation à un signe près

Définition 2.7: Champs qui dérivent d’un potentiel §

Soient $\Omega \subset {\mathbb{R}}^n$ un ensemble ouvert, et $F\in C^0(\Omega ;{\mathbb{R}}^n)$. Alors, le champ vectoriel $F$ dérive du potentiel $f\in C^1(\Omega )$ si $F=\nabla f$.

Proposition 2.8 §

Si $F\in C^1(\Omega ;{\mathbb{R}}^n)$ dérive du potentiel $f\in C^1(\Omega )$ et $\Gamma$ est une courbe régulière de paramétrisation $\gamma :[a,b]\mapsto \Omega$, alors:

$${\int }_{\Gamma }F\bullet d\ell =f(\gamma (b))-f(\gamma (a))$$

Théorème 2.10 §

Soient $\Omega \subset {\mathbb{R}}^n$ un ensemble ouvert, et $F\in C^1(\Omega ;{\mathbb{R}}^n)$. Condition nécessaire: si $F$ dérive d’un potentiel sur $\Omega$ alors

$$\begin{array}{rl}\frac{\partial F_i}{\partial x_j}\left(x\right)-\frac{\partial F_j}{\partial x_i}\left(x\right)& =0,\forall i,j=1,\cdots ,n\text{ et }\forall x\in \Omega .\end{array}$$

Condition suffisante: si la condition précédente est vérifiée et que $\Omega$ est simplement connexe, alors $F$ dérive d’un potentiel

Théorème 2.12: §

Soient $\Omega \subset {\mathbb{R}}^n$ un ensemble ouvert, et $F\in C^0(\Omega ;{\mathbb{R}}^n)$ un champ vectoriel. Alors les affirmations suivantes sont équivalentes:

1. $F$ dérive d’un potentiel sur $\Omega$
2. $\forall A,B\in \Omega$ et ${\Gamma }_1,{\Gamma }_2\subseteq \Omega$ des courbes régulières joignant A à B on a

$${\int }_{{\Gamma }_1}F\cdot d\ell ={\int }_{{\Gamma }_2}F\cdot d\ell .$$

3. ${\int }_{\Gamma }F\cdot d\ell =0$ pour toute courbe $\Gamma$ fermée simple régulières

Remarque 2.13: Marche à suivre pour répondre à la question “est-ce que $f$ dérive d’un potentiel?” §

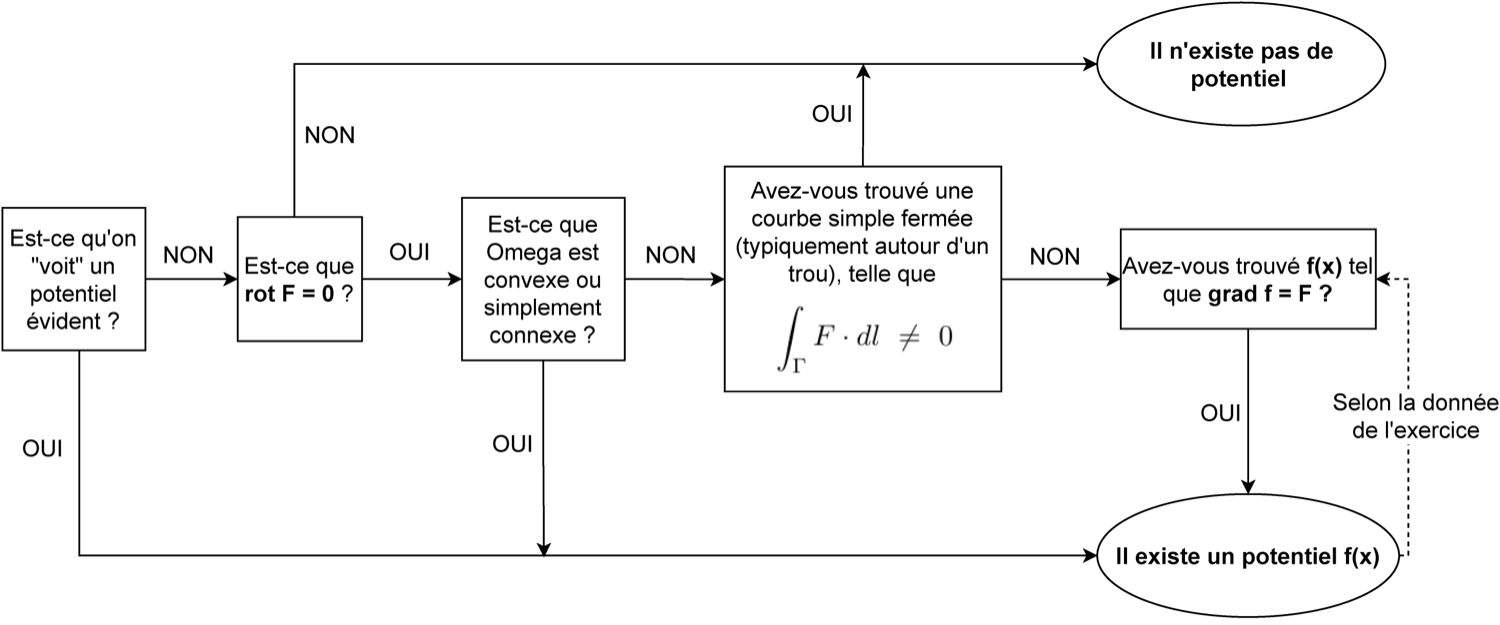REPONSES JAMAIS ACCEPTEES:

• $F$ ne dérive pas d’un potentiel car je ne trouve pas de $f$ tel que $\nabla f=F$
• $F$ dérive d’un potentiel car je ne trouve pas de $\Gamma \subseteq \Omega$ régulière fermée telle que ${\int }_{\Gamma }F\bullet d\ell \ne 0$

Définition 2.15: Bord, adhérence, bord orienté positivement/négativement, domaine régulier §

1. Soit $\Omega \subseteq {\mathbb{R}}^n$ un ouvert borné. Le bord de $\Omega$ noté $\partial \Omega$ est

$$\partial \Omega =\left\{x\in {\mathbb{R}}^n|\forall r>0,B_r(x)\cap \Omega \ne \varphi \text{ et }{B}_r(x)\cap {\Omega }^C\ne \varphi \right\}$$

où $B_r(x)$ est la boule ouverte de rayon $r$ centrée en $x$. On note $\bar{\Omega }=\Omega \cup \partial \Omega$ l’adhérence de $\Omega$

2. Soit $\Omega \subseteq {\mathbb{R}}^2$ un ouvert borné tel que $\partial \Omega$ est une courbe simple fermée régulière. Le bord $\partial \Omega$ est orienté positivement si les paramétrisations choisies laissent le domaine $\Omega$ à gauche.

3. $\Omega \subseteq {\mathbb{R}}^2$ un ouvert borné est un domaine régulier si il existe des ouverts bornés ${\Omega }_0,{\Omega }_1,\dots ,{\Omega }_n$ tq

   • ${\bar{\Omega }}_i\subseteq {\Omega }_0$ pour tout $1\le i\le k$.
   • ${\bar{\Omega }}_i\cap {\bar{\Omega }}_j=\varphi$ pour $1\le i<j\le k.$
   • $\partial {\Omega }_i$ est une courbe régulière simple fermée pour tout $0\le i\le k.$
   • $\Omega ={\Omega }_0\setminus {\bigcup }_{i=1}^k{\Omega }_i$

Théorème 2.16: Théorème de Green §

Soit $\Omega \subseteq {\mathbb{R}}^2$ un domaine régulier avec le bord $\partial \Omega$ orienté positivement. Soit aussi $F\in C^1(\Omega ;{\mathbb{R}}^2).$ Alors :

$${\iint }_{\Omega }\mathrm{rot}F(x,y)dxdy={\int }_{\partial \Omega }F\bullet d\ell$$

Remarques 2.17: §

1. On retrouve bien la structure

$${\int }_{\text{inteˊrieur}}\text{deˊriveˊes}={\int }_{\text{bord}}\text{fonction}$$

ce qui est similaire au théorème fondamental du calcul intégral.

$${\int }_a^b{f}^{\prime }(x)=f(b)-f(a)$$

2. Si $F$ dérive d’un potentiel, le théorème se lit $0=0$

Définition 2.19: Normale extérieure §

Soit $\Omega \subseteq {\mathbb{R}}^2$ un domaine régulier, $x_0\in \partial \Omega$. ${\nu }_{x_0}\in {\mathbb{R}}^2$ est la normale extérieure unité si

1. $|{\nu }_{x_0}|=1$
2. Si $\gamma :[a,b]\mapsto \partial \Omega$ est une paramétrisation telle que $\gamma (t_0)$ existe (où $t_0$ est tel que $\gamma (t_0)=x_0)$, alors $⟨{\gamma }^{\prime }(t_0),{\nu }_{x_0}⟩=0$.
3. Pour tout $\epsilon >0$ suffisamment petit, alors $x_0+\epsilon {\nu }_{x_0}\notin \Omega$

Si $\Omega$ est un domaine régulier de bord régulier orienté positivement, et $\gamma :[a,b]\mapsto \partial \Omega$ est une paramétrisation régulière, alors pour tout $t\in [a,b],$ nous avons :

$${\nu }_{\gamma (t)}=\frac{({\gamma }_2^{\prime }(t),-{\gamma }_1^{\prime }(t))}{\Vert {\gamma }^{\prime }(t)\Vert }$$

Corollaire 2.20: Le théorème de la divergence dans le plan §

Soit $\Omega \subset {\mathbb{R}}^2$ régulier, $F\in C^1(\Omega ;{\mathbb{R}}^2)$ un champ vectoriel, et $\nu$ la normale extérieure à $\Omega$. Alors, nous avons: ${\iint }_{\Omega }\mathrm{div}Fdxdy={\int }_{\partial \Omega }(F\bullet \nu )d\ell$

Remarque 2.22 §

1. Si $\Gamma$ est une partie du bord de $\Omega$ de paramétrisation $\gamma :[a,b]\to {\mathbb{R}}^2$ on a:

$${\int }_{\Gamma }F\bullet \nu d\ell ={\int }_a^{b}F(\gamma (t))\bullet ({\gamma }_2^{\prime }(t),-{\gamma }_1^{\prime }(t))dt$$

2. Si $\Gamma$ est une partie du bord sur laquelle je connais la normale extérieure, ${\int }_{\Gamma }F\bullet \nu d\ell$ ne dépend pas du sens de parcours car c’est l’intégrale curviligne d’un champs scalaire. Quelques courbes dont on connait la normale:
   • les segments de droite
   • les arcs de cercle centrés en 0

Corollaire 2.24: Formules d’aire: §

Soit $\Omega \subseteq {\mathbb{R}}^2$ un domaine régulier, $F,G_1,G_2\in C^{\infty }(\bar{\Omega };{\mathbb{R}}^2)$ définis par: $F(x,y)=(-y,x);G_1(x,y)=(0,x);G_2(x,y)=(-y,0)$. Alors:

$$\text{Aire}(\Omega )={\iint }_{\Omega }dxdy=\frac{1}{2}{\int }_{\partial \Omega }F\bullet d\ell ={\int }_{\partial \Omega }{G}_1\bullet d\ell ={\int }_{\partial \Omega }{G}_2\bullet d\ell$$

Corollaire 2.25: Identités de Green dans ${\mathbb{R}}^2$: §

Soit $\Omega \subseteq {\mathbb{R}}^2$ un domaine régulier, $\nu$ sa normale extérieure unité et $u,v\in C^2(\bar{\Omega })$

$${\iint }_{\Omega }\Delta u(x,y)dxdy={\int }_{\partial \Omega }\left(\nabla u\cdot \nu \right)d\ell .$$ $${\iint }_{\Omega }\left[v(x,y)\Delta u(x,y)+(\nabla u(x,y)\cdot \nabla v(x,y))\right]dxdy={\int }_{\partial \Omega }\left(v\nabla u\cdot \nu \right)dl$$ $${\iint }_{\Omega }\left(u(x,y)\Delta v(x,y)-v(x,y)\Delta u(x,y)\right)dxdy={\int }_{\partial \Omega }\left[u\left(\nabla v\cdot \nu \right)-v\left(\nabla u\cdot \nu \right)\right]dl$$