Chapitre 4: Les séries de Fourier §

4.1: Motivations, rappels et résultats préliminaires §

Taylor: §

$$f\in C^{\infty }\stackrel{?}{\to }f(x)=\sum _{k=0}^{\infty }{a}_k{\left(x-x_0\right)}^k.$$

Fourier: §

$$\begin{array}{rl}f,2\pi -\text{peˊriodique}\stackrel{?}{\to }f(x)& =\sum _{k=0}^{\infty }(a_k\cos (kx)+b_k\sin (kx))\\ & =a_0+\sum _{k=1}^{\infty }\left(a_k\cos (kx)+b_k\sin (kx)\right)\end{array}$$

Définition 4.1: Continuité par morceaux, $C^1$ par morceaux §

Soient $a<b,f:[a,b]\to \mathbb{R}$. $f$ est continue par morceaux et on note $f\in C_{\text{morc}}^0[a,b]$ si il existe $n\in \mathbb{N},a=a_0<a_1<\dots <a_n=b$ tel que $\forall i=1,\dots ,n,f\in C^0[a_{i-1},a_i]$ et ${\lim }_{x\to a_{i-1}^{+}}f(x)\stackrel{\text{deˊf}}{=}f(a_{i-1}^{+}),{\lim }_{x\to a_i^{-}}f(x)\stackrel{\text{deˊf}}{=}f(a_i^{-})$ existent et sont finies. Si de plus $f\in C^1[a_{i-1},a_i]$ et $f^{\prime }(a_i^{\pm })$ existent et sont finies, alors $f$ est $C^1$ par morceaux et on note $f\in C_{\text{morc}}^1[a,b]$

Par exemple, la fonction de gauche est continue par morceau, mais pas celle de droite puisque toutes les limites à gauche n’existent pas (à cause de l’asymptote verticale) :

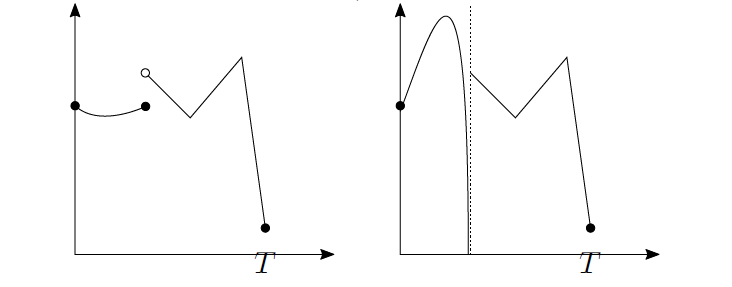
Proposition 4.2: §

Soient $n,m\in {\mathbb{N}}_{\ge 1},T>0$. Alors

$$\frac{2}{T}{\int }_0^T\cos \left(\frac{2\pi }{T}nx\right)\cos \left(\frac{2\pi }{T}mx\right)dx=\frac{2}{T}{\int }_0^T\sin \left(\frac{2\pi }{T}nx\right)\sin \left(\frac{2\pi }{T}mx\right)dx=\{\begin{array}{l}1\text{ si }n=m\\ 0\text{ sinon}\end{array}$$ $${\int }_0^T\sin \left(\frac{2\pi }{T}nx\right)\cos \left(\frac{2\pi }{T}mx\right)dx=0.$$

Remarque 4.3 §

$V=\{f:\mathbb{R}\to \mathbb{R}|f\in C_{\text{morc}}^1,f2\pi -\text{peˊriodique}\}$ est un espace vectoriel. On le munit du produit scalaire

$$⟨f,g⟩=\frac{1}{\pi }{\int }_0^{2\pi }f(x)g(x)dx$$

Ce que la proposition 4.2 nous dit est que $L=\{\sin (nx)|n\in {\mathbb{N}}_{\ge 1}\}\cup \{\cos (nx)|n\in {\mathbb{N}}_{\ge 1}\}$ est une liste orthonormale

Proposition 4.4: §

Soit $f:\mathbb{R}\to \mathbb{R},T-\text{peˊriodique}$, continue par morceaux. Alors $\forall a\in \mathbb{R}$,

$${\int }_a^{a+T}f(x)dx={\int }_0^{T}f(x)dx$$

4.2: Définition et convergence des séries de Fourrier §

Soit $f:\mathbb{R}\to \mathbb{R}$ T-périodique. Si je peux écrire $f(x)=a_0+{\sum }_{k=1}^{\infty }\left({\alpha }_k\cos (\frac{2\pi }{T}kx)+{\beta }_k\sin (\frac{2\pi }{T}kx)\right)$ Comment trouver ${\alpha }_k$ et ${\beta }_k$ ? On choisit

$$\begin{array}{rl}{\alpha }_k& =⟨f,\cos \left(\frac{2\pi }{T}kx\right)⟩\\ & =\frac{2}{T}{\int }_0^{T}f(x)\cos \left(\frac{2\pi }{T}kx\right)dx\end{array}$$ $$\begin{array}{rl}{\beta }_k& =⟨f,\sin \left(\frac{2\pi }{T}kx\right)⟩\\ & =\frac{2}{T}{\int }_0^{T}f(x)\sin \left(\frac{2\pi }{T}kx\right)dx\end{array}$$

Définition 4.5: Coefficients de Fourier réels, somme partielle de Fourier et les séries de Fourier §

Soit $f:\mathbb{R}\to \mathbb{R}$ continue par morceaux, T-périodique, les coefficients de Fourier réels de $f$ sont définis par: $\forall n>0$

$$a_n=\frac{2}{T}{\int }_0^{T}f(x)\cos \left(\frac{2\pi }{T}nx\right)dx$$ $$b_n=\frac{2}{T}{\int }_0^{T}f(x)\sin \left(\frac{2\pi }{T}nx\right)dx$$

La somme partielle de Fourier de $f$ et d’ordre $N$ est

$$F_{N}f(x)=\frac{a_0}{2}+\sum _{n=1}^N\left\{a_n\cos \left(\frac{2\pi }{T}nx\right)+b_n\sin \left(\frac{2\pi }{T}nx\right)\right\}$$

La série de Fourier de $f$

$$Ff(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left\{a_n\cos \left(\frac{2\pi }{T}nx\right)+b_n\sin \left(\frac{2\pi }{T}nx\right)\right\}$$

si elle converge

Théorème 4.7: Théorème de Dirichlet §

Soit $f:\mathbb{R}\to \mathbb{R}$ T-périodique $C^1$ par morceaux. Alors $\forall x\in \mathbb{R}$

$$Ff(x)=\frac{f(x-0)+f(x+0)}{2}=\underset{t\to 0}{\lim }\frac{f(x-t)+f(x+t)}{2}$$

Remarque 4.8: §

1. En réalité, l’hypothèse du théorème est plus faible que ça
2. Ca nous donne un outil pour faire deux choses
   1. Approximer une fonction avec des fonctions $C^{\infty }$
   2. Calculer des séries

Définition 4.10: Coefficients de Fourier complexes §

Soit $f:\mathbb{R}\to \mathbb{R}$ T-périodique $C_{\text{morc}}^0.$ On définit les coefficients de Fourier complexes par

$$c_n=⟨f,e^{i\frac{2\pi }{T}nx}⟩=\frac{1}{T}{\int }_0^{T}f(x)e^{-i\frac{2\pi }{T}nx}dx,\text{ pour }n\in \mathbb{Z}$$

où pour $\phi :\mathbb{R}\to \mathbb{C}$,

$${\int }_a^b\phi (x)dx={\int }_a^b\Re (\phi (x))dx+i{\int }_a^b\Im (\phi (t))dx.$$

Proposition 4.11: §

Soit $f:\mathbb{R}\to \mathbb{R}$ T-périodique $C_{\text{morc}}^0.$ Alors, 1)

$$\begin{array}{rl}\forall n\ge 1,c_n& =\frac{a_n-i{b}_n}{2}\\ \forall n\le -1,c_n& =\frac{a_{-n}+i{b}_{-n}}{2}\\ c_0& =\frac{a_0}{2}\end{array}$$

$$\begin{array}{rl}\forall n\ge 1,a_n& =c_n+c_{-n}\\ b_n& =i(c_n-c_{-n})\\ a_0& =2c_0\end{array}$$

$$\begin{array}{c}{F}_{N}f\left(x\right)=\sum _{n=-N}^N{c}_n{e}^{i\frac{2\pi }{T}nx}\\ Ff(x)=\sum _{n=-\infty }^{+\infty }{c}_n{e}^{i\frac{2\pi }{T}nx}=\underset{N\to +\infty }{\lim }\sum _{n=-N}^N{c}_n{e}^{i\frac{2\pi }{T}nx}\end{array}$$

4.3: Propriétés des séries de Fourier §

Proposition 4.12: §

Soit $f:\mathbb{R}\to \mathbb{R}$ un fonction T-périodique $C_{\text{morc}}^0.$ Alors,

1. La série de Fourier de $f$, $Ff$ est T-périodique
2. Si $f$ est paire (i.e $f(-x)=f(x)$), $b_n=0\forall n\ge 1$ et

$$Ff(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos \left(\frac{2\pi }{T}nx\right)$$

3. Si $f$ est impaire (i.e $f(-x)=-f(x)$), $a_n=0\forall n\ge 0$ et

$$Ff(x)=\sum _{n=1}^{\infty }{b}_n\sin \left(\frac{2\pi }{T}nx\right)$$

Proposition 4.13: Série de Fourier en cosinus §

Soit $L>0,f:[0,L]\to \mathbb{R}$ une fonction $C_{\text{morc}}^1$ et la série

$$F_{C}f(x)=\frac{\widetilde{a_o}}{2}+\sum _{n=1}^{\infty }\widetilde{a_n}\cos \left(\frac{\pi }{L}nx\right)$$

où

$$\widetilde{a_n}=\frac{2}{L}{\int }_0^{L}f(x)cos\left(\frac{\pi }{L}nx\right)dx$$

Alors $F_{C}f$ converge vers

$$F_{C}f(x)=\{\begin{array}{ll}\frac{f(x-0)+f(x+0)}{{}^2}& \text{si }x\in ]0,\mathrm{L}[\\ f(0+0)& \text{si }x=0\\ f(L-0)& \text{si }x=L.\end{array}$$

Proposition 4.14: Série de Fourier en sinus §

Soit $L>0,f:[0,L]\to \mathbb{R}$ une fonction $C_{\text{morc}}^1$ et la série

$$F_{S}f(x)=\sum _{n=1}^{\infty }{\tilde{b}}_n\sin \left(\frac{\pi }{L}nx\right)$$

où

$$\begin{array}{r}{\tilde{b}}_n=\frac{2}{L}{\int }_0^{L}f(x)\sin \left(\frac{\pi }{L}nx\right)dx\end{array}$$

Alors $F_{S}f$ converge vers

$$F_{S}f(x)=\{\begin{array}{ll}\frac{f(x-0)+f(x+0)}{{}^2}& \text{si }x\in ]0,\mathrm{L}[\\ 0& \text{si }x=0\text{ ou }x=L\end{array}$$

Théorème 4.16: L’identité de Parseval §

Soit $f:\mathbb{R}\to \mathbb{R}$ une fonction $C_{\text{morc}}^1$. Alors,

$$\frac{2}{T}{\int }_0^T{f}^2(x)dx=\frac{a_0^2}{2}+\sum _{n=1}^{+\infty }(a_n^2+b_n^2)=2\sum _{n\in \mathbb{Z}}|c_n{|}^2$$

où $\{a_n\},\{b_n\}$ sont les coefficients de Fourier réels de F et $\{c_n\}$ sont les coefficients complexes

Remarque 4.17: §

1. Le théorème reste vrai si on affaiblit l’hypothèse, $|f|,f^2$ sont intégrables sur $[0,T]$, le résultat reste vrai
2. Une deuxième méthode pour calculer des séries

Remarque 4.19: §

Un exercice typique sur les séries de Fourier est la donnée d’une fonction $f:\mathbb{R}\to \mathbb{R}$ T-périodique et des questions:

• Calculer la série de Fourier de f
• En déduire la valeur d’une série ${\sum }_{n=1}^{\infty }{\phi }_n$

Pour déduire la valeur de la série ${\sum }_{n=1}^{\infty }{\phi }_n$ on a deux possibilités:

• Théorème de Dirichlet
• Identité de Parseval Indicateur pour savoir quelle méthode choisir: Comparer l’ordre de $n$ dans $a_n$ et $b_n$ et l’ordre de $n$ dans ${\phi }_n$
• Si ordre $a_n$ et $b_n$ = ordre ${\phi }_n$ => Théorème de Dirichlet
• Si 2 $\times$ ordre $a_n$ et $b_n$ = ordre ${\phi }_n$ => Identité de Parseval

Proposition 4.20: Dérivation et intégration terme à terme des séries de Fourier §

Soit $f:\mathbb{R}\to \mathbb{R}$, T-périodique, continue, $C_{\text{morc}}^1$ telle que $f^{\prime }\in C_{\text{morc}}^1$. Alors

$$F{f}^{\prime }=\sum _{n=1}^{\infty }\frac{2\pi }{T}n\left\{-a_n\sin \left(\frac{2\pi }{T}nx\right)+b_n\cos \left(\frac{2\pi }{T}nx\right)\right\}=\frac{f^{\prime }(x-0)+f^{\prime }(x+0)}{2}$$

où $\{a_n\}$ et $\{b_n\}$ sont les coefficients de Fourier de $f$

Remarque 4.21 §

$f^{\prime }$ n’est en fait pas définie partout. Il y a des points isolés où $f$ n’est pas définie (là ou $f$ n’est pas dérivable). Ca n’est plus un problème car:

1. Si je calcule les coefficients de Fourier de $f^{\prime }$, je calcule des intégrales. Et ce qui se passe sur un point isolé est négligeable
2. $\frac{f^{\prime }(x-0)+f^{\prime }(x+0)}{2}$ est défini partout!

Remarque 4.21.2 §

$f$ est $T$-périodique $⟹$ $f^{\prime }$ est $T$-périodique

$f$ est $T$-périodique et $F^{\prime }=f$ $/⟹$ $F$ est $T$-périodique

$f$ est $T$-périodique et ${\int }_0^{T}f(x)dx=0$ et $F^{\prime }=f$ $⟹$ $F$ est $T$-périodique