Chapitre 3: Intégrales de surface §

Notation 3.1: §

A partir de maintenant on se permet d’écrire les composantes de nos applications avec les indices en haut:

$$G(\bar{x})=(G^1(\bar{x}),G^2(\bar{x}),\dots ,G^n(\bar{x}))$$

On écrira aussi pour $f:{\mathbb{R}}^3\to \mathbb{R}$

$$f_x(x,y,z)=\frac{\partial f}{\partial x}(x,y,z),f_y(x,y,z)=\frac{\partial f}{\partial y}(x,y,z),f_z(x,y,z)=\frac{\partial f}{\partial z}(x,y,z)$$

Définition 3.2: Surface régulière §

$\Sigma \subseteq {\mathbb{R}}^3$ est une surface régulière si:

1. $\exists A\subseteq {\mathbb{R}}^2$ un ouvert borné tel que $\partial A$ est une courbe simple fermée régulière (par morceaux) et $\sigma :\bar{A}\to {\mathbb{R}}^3:(u,v)\to \sigma (u,v)=({\sigma }^1(u,v),{\sigma }^2(u,v),{\sigma }^3(u,v))$ telle que

   • $\sigma \in C^1(\bar{A},{\mathbb{R}}^3)$
   • $\sigma (\bar{A})=\Sigma$
   • $\sigma$ est injective sur $A$
2. 
   $$\begin{array}{r}\overrightarrow{{\sigma }_u}\wedge \overrightarrow{{\sigma }_v}=\left|\begin{array}{ccc}{\bar{e}}_1& {\bar{e}}_2& {\bar{e}}_3\\ {\sigma }_u^1& {\sigma }_u^2& {\sigma }_u^3\\ {\sigma }_v^1& {\sigma }_v^2& {\sigma }_v^3\end{array}\right|=\left[\begin{array}{c}{\sigma }_u^2{\sigma }_v^3-{\sigma }_v^2{\sigma }_u^3\\ {\sigma }_v^1{\sigma }_u^3-{\sigma }_u^1{\sigma }_v^3\\ {\sigma }_v^2{\sigma }_u^1-{\sigma }_u^2{\sigma }_v^1\end{array}\right]\end{array}$$

   est tel que $|{\sigma }_u\wedge {\sigma }_v|\ne 0\forall (u,v)\in A$

$\sigma$ est une paramétrisation régulière de $\Sigma$ et $\frac{{\sigma }_v\wedge {\sigma }_u}{|{\sigma }_v\wedge {\sigma }_u|}={\nu }_{(u,v)}$ est la normale unité au point ${\sigma }_{(u,v)}$

Définition 3.4: Surface orientable §

Une surface régulière $\Sigma \subseteq {\mathbb{R}}^3$ est orientable si il existe un champ de vecteurs normaux unitaires continus

$$\nu :\Sigma \to {\mathbb{R}}^3$$

La donnée d’un tel champ est appelée une orientation de $\Sigma$

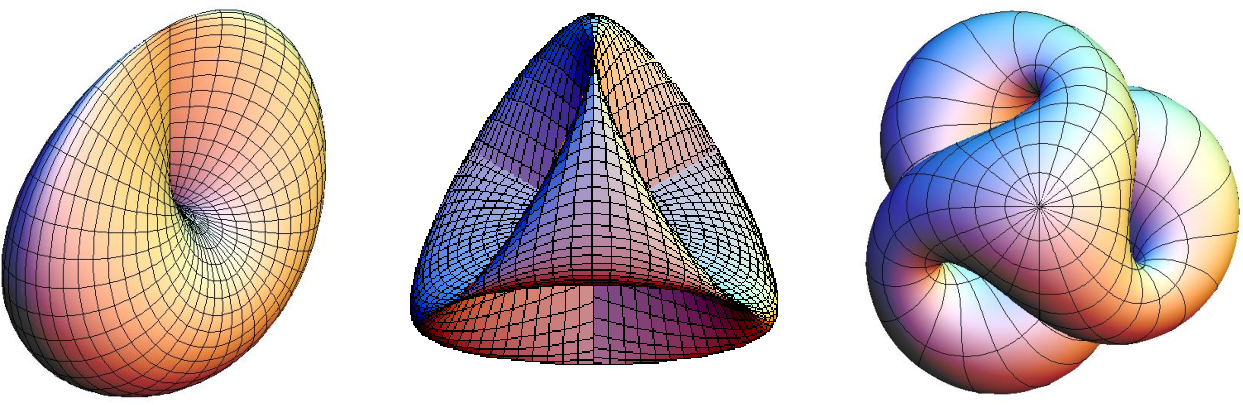
Figure ci dessus: Surfaces non-orientables

Remarque 3.5: §

Les problèmes avec la continuité de $\nu$ peut survenir au “recollement”. C’est à dire sur les parties de $\partial \mathcal{A}$ où $\sigma$ n’est pas injective. Les surfaces non orientables sont très rares.

Définition 3.6: Intégrale de surface §

Soit $\Omega \subseteq {\mathbb{R}}^3$ un ouvert, $f\in C^0(\Omega ),F\in C^0(\Omega ;{\mathbb{R}}^3),\Sigma \subseteq \Omega$ une surface orientable paramétrée par $\sigma :\bar{\mathcal{A}}\to \Sigma :(u,v)\mapsto \sigma (u,v)$ L’intégrale de $f$ sur $\Sigma$ est définie par

$${\iint }_{\Sigma }fdS={\iint }_{A}f(\sigma (u,v))\Vert {\sigma }_u\wedge {\sigma }_v\Vert dudv$$

L’intégrale de $F$ sur $\Sigma$ est définie par

$${\iint }_{\Sigma }F\bullet dS={\iint }_{A}F(\sigma (u,v))\bullet ({\sigma }_u\wedge {\sigma }_v)dudv$$

Si $\Sigma ={\bigcup }_{i=1}^k{\Sigma }_i$ est une surface régulière par morceaux avec ${\Sigma }_i$ régulière orientable,

$${\iint }_{\Sigma }fdS=\sum _{i=1}^k{\iint }_{{\Sigma }_i}fdS,{\iint }_{\Sigma }F\bullet dS=\sum _{i=1}^k{\iint }_{{\Sigma }_i}F\bullet dS$$

Remarque 3.7: §

En comparant avec l’intégrale curviligne,

$$\gamma ⟷\sigma ,{\gamma }^{\prime }(t)⟷{\sigma }_u\wedge {\sigma }_v$$

L’intégrale de surface d’un champ scalaire ne dépend pas du choix de la paramétrisation. Le signe de l’intégrale de surface d’un chams vectoriel dépend de l’orientation de ${\sigma }_u\wedge {\sigma }_v$ i.e le choix d’orientation de $\Sigma$, plus précisément ud choix entre ${\sigma }_u\wedge {\sigma }_v$ et ${\sigma }_v\wedge {\sigma }_u$

Définition 3.9: Domaine régulier de ${\mathbb{R}}^3$ §

Soit $\Omega \in {\mathbb{R}}^3$ un ouvert borné. $\Omega$ est un domaine régulier s’il existe des ouverts bornés ${\Omega }_0,\dots ,{\Omega }_m$ tels que :

1. $\overline{{\Omega }_i}\subseteq {\Omega }_0$ pour $1\le i\le m$.
2. $\overline{{\Omega }_i}\cap \overline{{\Omega }_j}=\varphi$ pour $1\le i<j\le m$
3. $\Omega ={\Omega }_0\setminus {\bigcup }_{i=1}^k\overline{{\Omega }_i}$
4. $\partial {\Omega }_i={\Sigma }_i$ est une surface régulière par morceaux orientable

Théorème 3.10: Théorème de la divergence §

Soient $\Omega \subset {\mathbb{R}}^3$ régulier, $F\in C^1(\overline{\Omega },{\mathbb{R}}^3)$ $\nu$ un champ de normales extérieures à $\Omega$ continu. Alors:

$${\iiint }_{\Omega }\mathrm{div}(F)dxdydz={\iint }_{\partial \Omega }(F\bullet \nu )dS$$

Remarque 3.12 §

Si $\Sigma$ est une partie du bord de $\Omega$ paramétrée par $\sigma$, alors

$$\begin{array}{rl}{\iint }_{\Sigma }(F\bullet \nu )dS& ={\iint }_A(F\bullet \nu )\Vert {\sigma }_u\wedge {\sigma }_v\Vert dudv\\ & =\pm {\iint }_{A}F\bullet \frac{({\sigma }_u\wedge {\sigma }_v)}{\Vert {\sigma }_u\wedge {\sigma }_v\Vert }\Vert {\sigma }_u\wedge {\sigma }_v\Vert dudv\\ & =\pm {\iint }_{A}F\bullet ({\sigma }_u\wedge {\sigma }_v)dudv\\ & =\pm {\iint }_{\Sigma }F\bullet dS\\ & {\iint }_{\Sigma }(F\bullet \nu )dS=\pm {\iint }_{\Sigma }F\bullet dS\end{array}$$

où le signe $\pm$ est choisi de telle sorte que $\pm {\sigma }_u\wedge {\sigma }_v$ est un vecteur normal extérieur

Corollaire 3.13: Formules d’aire §

Soit $\Omega \subseteq {\mathbb{R}}^3$ un domaine régulier et $\nu :\partial \Omega \to {\mathbb{R}}^3$ un champ de normales extérieures unités continu. Soient encore les champs vectoriels $F(x,y,z)=(x,y,z);G_1(x,y,z)=(x,0,0);$ $G_2(x,y,z)=(0,y,0);G_3(x,y,z)=(0,0,z)$ Alors:

$$\text{Volume}(\Omega )=\frac{1}{3}{\iint }_{\partial \Omega }(F\bullet \nu )dS={\iint }_{\partial \Omega }(G_i\bullet \nu )dS$$

Corollaire 3.14: Identités de Green §

Soit $\Omega \subseteq {\mathbb{R}}^3$ un domaine régulier , $f,g\in C^2(\bar{\Omega })$ $\nu :\partial \Omega \to {\mathbb{R}}^3$ un champ de normales extérieures unités continu. Alors:

$${\iiint }_{\Omega }(\Delta f)dxdydz={\iint }_{\partial \Omega }⟨\nabla f;\nu ⟩ds$$ $${\iiint }_{\Omega }(f\Delta g+⟨\nabla f;\nabla g⟩)dxdydz={\iint }_{\partial \Omega }⟨f\nabla g;\nu ⟩ds$$ $${\iiint }_{\Omega }(f\Delta g-g\Delta f)dxdydz={\iint }_{\partial \Omega }⟨f\nabla g-g\nabla f;\nu ⟩ds$$

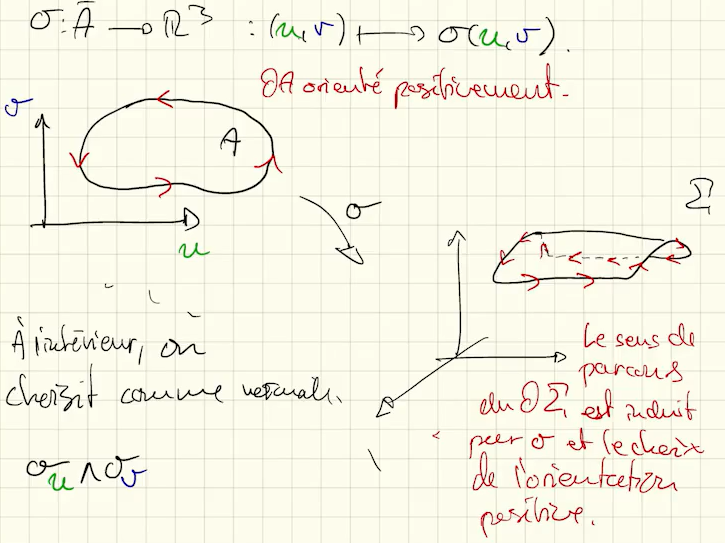
Définition 3.15: Bord d’une surface, sens de parcours induit par $\sigma$ §

Soit $\Sigma \subseteq {\mathbb{R}}^3$ une surface régulière orientable, $\sigma :\bar{\mathcal{A}}\to \Sigma$ une paramétrisation de cette surface

1. Si $\partial \mathcal{A}$ est une courbe simple, régulière, fermée alors:

$$\partial \Sigma =\sigma (\partial \mathcal{A})$$

et le choix d’un sens de parcours sur $\partial \mathcal{A}$ induit un sens de parcours sur $\partial \Sigma$ par composition avec $\sigma$: si $\gamma :[a,b]\to {\mathbb{R}}^2$ est une paramétrisation de $\partial \mathcal{A}$ (et donc, un choix de sens de parcours), $\sigma \circ \gamma :[a,b]\to {\mathbb{R}}^3$ est une paramétrisation de $\partial \Sigma$ et donc un choix de sens de parcours. Le sens de parcours de $\sigma \circ \gamma$ est le sens de parcours induit par $\sigma$ 2. Si $\partial \mathcal{A}$ contient une courbe simple fermée régulière par morceaux, le bord de $\Sigma$ est donné par $\sigma \partial \mathcal{A}$ dont on enlève: 1. Les bouts de courbes qui sont parcourues deux fois dans des directions opposés 2. Les bouts de courbes qui sont réduits à un point L’orientation induite par $\sigma$ est définie de manière analogue à ci-dessus

Remarques 3.17: §

1. Il n’existe pas de bonne notion de bord orienté positivement pour une surface $\Sigma \subseteq {\mathbb{R}}^3$
2. Fun fact: $\partial (\partial \Omega )=\varnothing$

Théorème 3.18: Théorème de Stokes §

Soit $\Omega \subseteq {\mathbb{R}}^3$ un ouvert, $\Sigma \subseteq \Omega$ une surface régulière orientable par morceaux, $F\in C^1(\overline{\Omega },{\mathbb{R}}^3)$. Alors

$${\iint }_{\Sigma }(\mathrm{rot}F)\bullet dS={\int }_{\partial \Sigma }F\bullet d\ell$$

Remarques 3.19: §

1. Le signe de ${\iint }_{\Sigma }(\mathrm{rot}F)\bullet dS$ dépend de l’orientation de $\Sigma$ (intégrale de surface d’un champ vectoriel). Le signe de ${\int }_{\partial \Sigma }F\bullet d\ell$ dépend du sens de parcours (intégrale curviligne d’un champ vectoriel). Astuce pour s’assurer que les choix qu’on fait sont compatibles:
2. ${\iint }_{\partial \Omega }(\mathrm{rot}F)\bullet dS=0\forall \Omega \subseteq {\mathbb{R}}^3\text{ domaine reˊgulier}$